Recursion in C Language with Example Programs

Introduction:

We have looked at the call by value and call by reference in our earlier posts, In today’s article, We are going to look at the recursion in c language with Example Programs.

Recursion in C language:

Function calling itself is called recursion. Any function which calls itself is called a recursive function.

If we have a complex problem, Then break down the complex problem into smaller and simpler problems. and try to solve those smaller problems(using a function and calling it repetitively) and finally add all these smaller problems to create the complete solution. It will make sense once we look at an example program.

The recursive functions are used extensively in data structures and algorithms, For example, To traverse a tree (inorder, preorder, and post-order traversal) we use the recursion.

Syntax of Recursive function:

Here is the syntax of the recursive function ( Recursion in C )

How does the recursion work in C Language? ( Recursive function call flow):

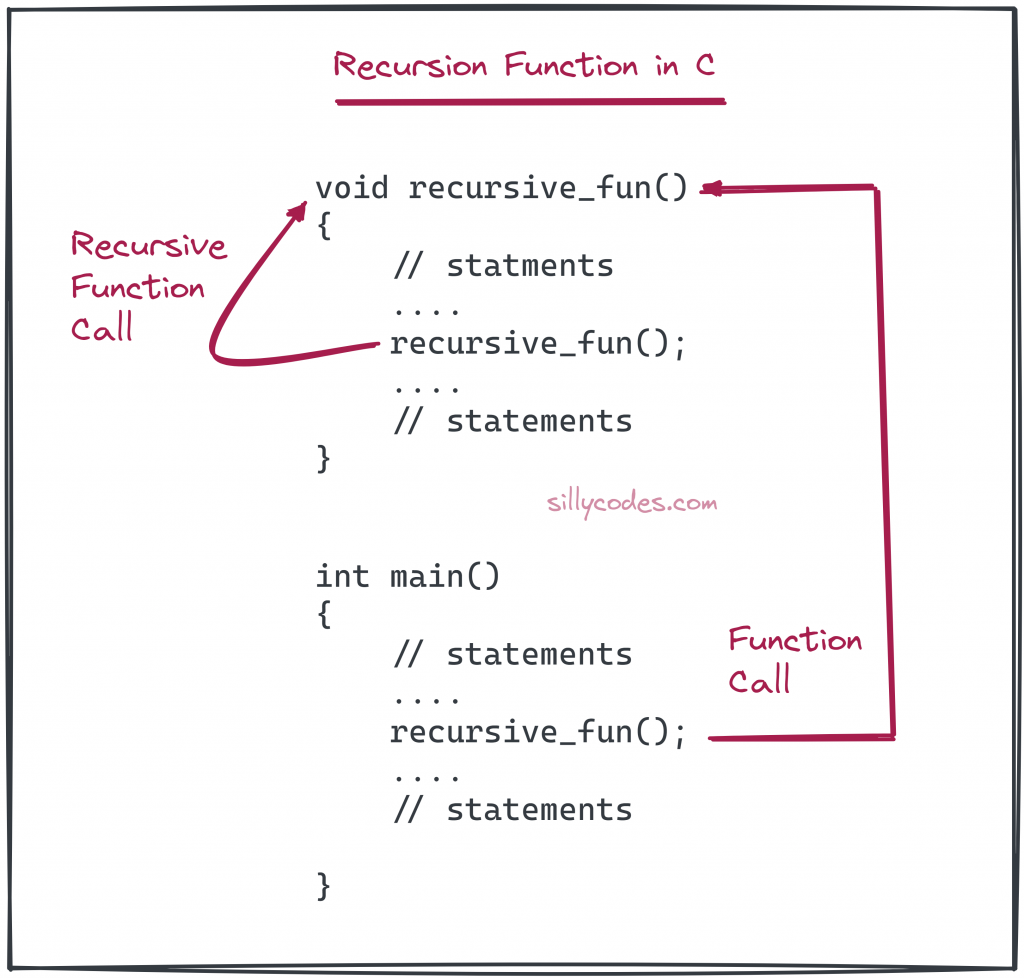
If we look at the above syntax of the recursive function, We can see that we called the recursive_fun() from the main() function. Which takes the program control to recursive_func().

Inside the body of the recursive_func(), We called the recursive_func() again. ( Function called itself). So we will execute the recursive_fun() again, which calls recursive_func() again. This process continues and creates an Infinite recursion.

To solve the Infinite recursion, We need to have the Base Condition or Exit condition for the recursive function. Typically we use if else statement to stop the recursion when a certain condition is met. ( so that function stops calling itself) and execution unravels back to the main().

For each recursive function call, One stack frame is pushed to the stack, Which contains the local variables, formal arguments, and return address of function. So recursive calls take memory in the RAM ( stack ).

To write a recursive function,

• We should be able to divide the problem into similar and smaller subtasks ( So that we can call the same function again and again)
• We should also decide the proper base condition for the recursion So that we can stop the recursion. Otherwise, we might get into the infinite recursion.

Let’s look at a couple of example programs to understand the recursion in the C programming language.

Example 1: Factorial of a number using Recursion in C Language:

Write a C Program to calculate the factorial of a number using the recursion.

We have already looked at the factorial of the number program earlier using the iterative method, In this program, we will calculate the factorial using the recursion.

Program Output:

Let’s compile and run the program.

Factorial of Number(fact) Recursive functions call flow:

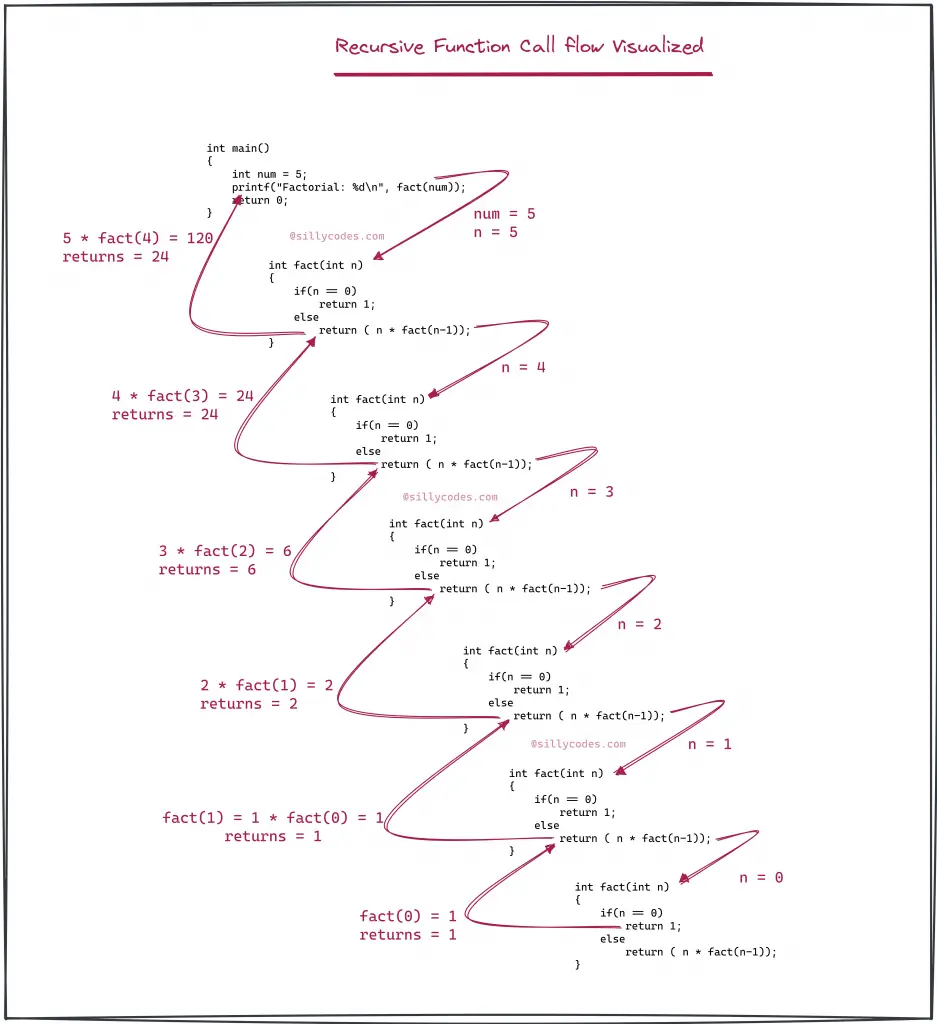
1. The main() function started by asking for the user input and we stored it in the variable num. Let’s say the user provided the num as the 5.
2. Then we called the fact function with the user input i.e fact(num) which fact(5)
3. The program counter jumped to fact() function and started executing the fact() function.
4. As we have learned earlier, To create the recursive function, We need to divide the problem into smaller subtasks and should have a base condition. Here the base condition is if(n == 0), As we know the Factorial of the number 0 is 1. So we know that we reached the end, So we can stop our recursion.
5. Call From main() function : The Initial value of the number n is not 0, which is 5( n=5), So the base condition won’t be executed and we go to the else statement. Where we used the return ( n * fact(n-1));, Here we are calling the fact function again, but this time, Instead of calling with n, We are calling it with n-1. And we are also multiplying the result of fact(n-1) with n.
   • return ( n * fact(n-1)); which is return ( 5 * fact(5-1));
6. First Recursive Call : The above fact(n-1) call creates a recursive call to fact function, As the value of n for the second call is 4, The base condition won’t be executed, We will go to the else statement again. Where we will call the fact function again with n=n-1 which is 3.
   • return ( 4 * fact(4-1) ); which is return ( 4 * fact(3) );
7. Second Recursive Call: In the next recursive call, The value of n will be 3, The base condition won’t be executed, We will go to the else statement again. Where we will call the fact function again with n=n-1 which is 2.
   • return ( 3 * fact(3-1) );which is return ( 3 * fact(2) );
8. Third Recursive Call: In the next recursive call, The value of n will be 2, The base condition won’t be executed, We will go to the else statement again. Where we will call the fact function again with n=n-1 which is 1.
   • return ( 2 * fact(2-1) );which is return ( 2 * fact(1) );
9. Fourth Recursive Call: In the next recursive call, The value of n will be 1, The base condition if(n == 0) won’t be executed, We will go to else statement again. Where we will call the fact function again with n=n-1 which is .
   • return ( 1 * fact(1-1) );which is return ( 1 * fact(0) );
10. Fifth Recursive Call: Now in this recursive call to fact function, The n value became . So our base condition if(n==0) will be True, As we reached the number = 0, We stop the recursion and return 1 ( As the factorial of is 1). Which takes the program control back to above step – 9.
    • This function returns 1
11. Now one by one each recursive function returns in the backward direction ( stack unwinding ) and returns n * fact(n-1)
    • Fifth call return 1
    • Fourth recursive call returns 1 * fact(0) which is 1 * 1 and fact(1) = 1, return 1
    • Third recursive call returns 2 * fact(1) which is 2 * 1 and return 2
    • Second recursive call returns 3 * fact(2) which is 3 * 2 and return 6
    • First recursive call returns 4 * fact(3) which is 4 * 6 and return 24
    • Call from main() function returns return ( 5 * fact(4)); which is equal to 5 * 24, i.e 120. So the function fact returns value 120 to the main() function.
12. The main() function gets 120 and prints on the console using the printf function.

Here is the pictorial representation of the Factorial Recursive function call flow or Stack flow:

Example 2: Sum of Digits of a Number using Recursion in C Language:

Let’s look at another program to make our understanding concrete. Write a C Program to calculate the sum of digits of a number using the recursive function.

Program Output:

Sum of Digits of a number recursive function Explanation:

1. The program starts by asking input number from the user and stores it in variable n. Let’s say the user provided the number 921.
2. Then main() function calls, The sumOfDigits function with n(which is 921) to get the sum of digits in the number n.
3. Call from Main() Function: sumOfDigits() function execution will start, and we used the if(n == 0) as our base condition. The base condition will be False, So we continue to the next statement.
4. Here return ( (n % 10) + sumOfDigits(n / 10) );, we are getting the last element from the given number n using the Modulus operator using n%10, Then we are calling the sumOfDigits function (Recursive call) and passing the n/10 ( which actually removes the last digit as we already processed it)
   • Let’s apply the example values – i.e n = 921
   • return ( (921 % 10) + sumOfDigits(921 / 10) );
   • return ( (1) + sumOfDigits(92) );
5. First Recursive Call: The sumOfDigits(92) creates a recursive call to sumOfDigits function. Now the n value is 92, So the base condition will be False, We go to the next statement and make another recursive call.
   • return ( (92 % 10) + sumOfDigits(92 / 10) );
   • return ( (2) + sumOfDigits(9) );
6. Second Recursive Call: The value of n is 9, So the base condition will be False, We will go to the next statement and makes another recursive call.
   • return ( (9 % 10) + sumOfDigits(9 / 10) );
   • return ( (9) + sumOfDigits(0) );
7. Third Recursive Call: The value of n is . So the base condition n == 0 will be executed and the sumOfDigits function returns with value .
8. Now all The functions start to return one by one in the backward direction, Here are the return values of each function
   • Second Recursive Call returns ( 9 + 0 ) which is 9
   • First Recursive Call returns ( 2 + 9 ) which is 11
   • The sumOfDigits function returns ( 1 + 11 ) which is 12. and sumOfDigits function returns value to main function.
9. Finally, the Main() function prints the result onto the console.

Advantages and disadvantages of Recursion:

• Recursion makes code compact and elegant.
• We can easily solve many data structures and algorithm problems using Recursion.
• Memory Usage: As we know, For each recursive function call, There will be a stack frame pushed to memory(Stack region), So there will be a memory overhead for recursion. If you use a high number of recursive calls, Then we might end up using a lot of extra RAM.
• The recursive function should have the appropriate base condition, Otherwise, We might create the Infinite recursive function.
• Recursion is slower compared to the iterative method (Loops) due to the cost of stack push and pops.
• Debugging the recursive functions is hard.

Conclusion:

We have looked at the Recursion in C Programming Language with Example Programs. We also looked at the recursive function call flow and how functions are pushed to the stack and how recursive functions return to create the final output. Finally, We looked at the advantages and disadvantages of the recursive functions (recursion in general).

Related Articles:

• C Functions
• Types of Functions
• Call by Value and Call by Reference in C

Related Programs:

• Arithmetic Operations using functions
• Fibonacci Series using function
• Factorial of a Number using functions
• Armstrong Number using Function in C language
• Prime number program using Function
• Program to Caclulate Area of Circle using Function
• Program to Check Even or Odd number using Function
• Binary to Decimal Conversion using function in C
• Arithmetic Operations using Functions
• Add Two Numbers using Function
• 100+ C Practice Programs
• C Tutorials Index