Program to Check Symmetric Matrix in C

Program Description:
Write a program to Check Symmetric Matrix in C programming language. The program will accept a Matrix from the user and check if it is a Symmetric Matrix.
What is a Symmetric Matrix?
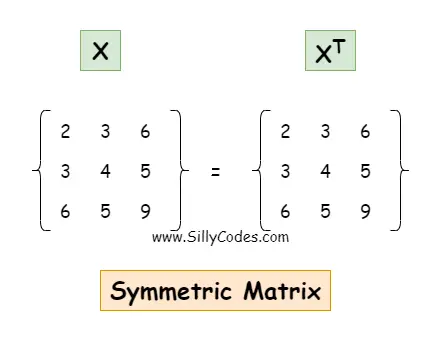
A Matrix is called a Symmetric Matrix When the Transpose of the Matrix is equal to the Original Matrix.
The Symmetric Matrix is a Square Matrix.
If a Matrix X is said to be symmetric when
X = XT
Where X is an Original Matrix and XT is the Transpose of the X.
Let’s look at an example to understand the symmetric matrix.
Original Matrix : X:
|
1 2 3 |
2 3 6 3 4 5 6 5 9 |
Transpose of X: XT
|
1 2 3 |
2 3 6 3 4 5 6 5 9 |
Here is the graphical representation of the symmetric matrix
Let’s look at an example program to check a symmetric matrix in the c programming language
Prerequisites:
It is recommended to know the Arrays in C language and Multi-dimensional arrays. Please go through the following articles to learn more about these topics.
- Multi-Dimensional Arrays in C
- Read and Print 2D Arrays in C
- Passing 2D Arrays to Functions
- One dimensional Arrays in C
Algorithm to check the Symmetric Matrix:
As the Symmetric matrix’s Transpose is equal to the Original Matrix. So we need to calculate the Transpose and compare the two matrices.
Step 1: Calculate the Transpose of the Matrix (XT)
Step 2: Check if the Transpose (XT) and Original Matrices(X) are Equal
Check Symmetric Matrix in C Program Explanation:
Here is a step-by-step explanation of the check symmetric matrix program.
- Create two integer constants named ROWS and COLUMNS, Which holds the max number of rows and columns in the Matrix. Please change this number if you want to play with the large arrays.
- Start the Program by declaring two Matrices (2D Arrays). They are X matrix, and XTranspose Matrix. The row size and column size of the matrices are ROWS and COLUMNS constants respectively.
- Prompt the user to provide the desired Row size and Column Size, and store them in the variables rows and columns respectively.
- The Symmetric matrix must be a Square Matrix. So check if the rows and columns are equal – if(rows != columns)
- Check for array bounds using the (rows >= ROWS || rows <= 0 || columns >= COLUMNS || columns <= 0) condition, And display an error message if the row/column sizeis beyond the present limits.
- Take the user input for Input Matrix i.e Matrix-X, We need to use two For Loops, One For Loop will iterate over the rows, and the Second For Loop will iterate over the columns
- Create the First For Loop ( Outer Loop), Start the iteration from i=0 and go till the i<rows (that is for(i=0; i<rows; i++) ). At Each iteration of the Outer Loop,
- Create the second For Loop ( Inner Loop). This loop is a Nested loop that will be inside the Outer Loop. Start the Loop from j=0 and go till the j<columns (i.e for(j=0; j<columns; j++) ). The Inner Loop will iterate over the columns. At each iteration of the Inner Loop
- Prompt the user to provide the Matrix element and Read the element using the scanf function and Update the X[i][j] element.
- Repeat the above step for all elements in the Matrix-X
- Create the second For Loop ( Inner Loop). This loop is a Nested loop that will be inside the Outer Loop. Start the Loop from j=0 and go till the j<columns (i.e for(j=0; j<columns; j++) ). The Inner Loop will iterate over the columns. At each iteration of the Inner Loop
- Now, To Calculate the Transpose of the X, We need to use two more for loops.
- Create Outer For Loop ( Iterates over
rows) – for(i=0; i<rows; i++)
- Then Create the Inner For loop (Iterates over
columns) – for(j=0; j<columns; j++)
- Copy the value of the X[i][j] element to the XTranspose[j][i]. Note that, i and j are interchanged.
- i.e XTranspose[j][i] = X[i][j];
- Then Create the Inner For loop (Iterates over
columns) – for(j=0; j<columns; j++)
- Once the step-8 is completed, The XTranspose Matrix contains the Transpose of the X (Matrix).
- Now, We need to Check if the two matrices (X and XTranspose) are Identical.
- Create Outer For Loop to iterate over rows – for(i=0; i<rows; i++)
- Create Inner For loop to iterate over columns – for(j=0; j<columns; j++), At Each Iteration,
- Check if the X[i][j] element is equal to XTranspose[i][j] element – if(X[i][j] != <code>XTranspose[i][j])
- If any element pair is not equal, Then Matrix X and XTranspose are not Identical. Thus Input Matrix X is not a Symmetric Matrix.
- Create Inner For loop to iterate over columns – for(j=0; j<columns; j++), At Each Iteration,
- If the Matrix X and XTranspose are Equal, Then Input matrix X is a Symmetric Matrix.
- Stop the Program.
Program to Check Symmetric Matrix in C Language using Loops:
Here is the program to check the symmetric matrix in the C programming language.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 |
/* Program to Calculate if the Matrix is Symmetric Matrix in C SillyCodes.com */ #include <stdio.h> // Define MAX ROWS and COLUMNS const int ROWS=100; const int COLUMNS=100; int main() { // Declare two matrices. // 'X' is Input matrice // 'XTranspose' stores Transpose of 'X' int X[ROWS][COLUMNS], XTranspose[ROWS][COLUMNS]; int rows, columns, i, j; // Take the Row size and Column size from user printf("Enter the Row size for Matrix(1-%d): ", ROWS); scanf("%d", &rows); printf("Enter the Column Size for Matrix(1-%d): ", COLUMNS); scanf("%d", &columns); // Check if the matrix is square if(rows != columns) { printf("Symmetric Matrix is Square Matrix, Rows and Columns Must be Equal \n"); return 0; } else if(rows >= ROWS || rows <= 0 || columns >= COLUMNS || columns <= 0) { // check for array bounds printf("Invalid Rows or Columns size, Please Try again \n"); return 0; } // Take the user input for 1st Matrix - 'X' printf("Enter Elements for the Matrix(X) of Size %dX%d: \n", rows, columns); for(i=0; i<rows; i++) { for(j=0; j<columns; j++) { // printf("X[%d][%d]: ", i, j); scanf("%d", &X[i][j]); } } // Transport the Matrix 'X' and store the result in `XTranspose' for(i=0; i<rows; i++) { for(j=0; j<columns; j++) { // Transpose X. Note, 'i' and 'j' are interchanged XTranspose[j][i] = X[i][j]; } } // Print the Result printf("Transpose of Maxtrix X(XTranspose = X^T) is : \n"); // Note, That we are iterating over columns and then rows for(i=0; i<columns; i++) { for(j=0; j<rows; j++) { // Print Elements printf("%d ", XTranspose[i][j]); } printf("\n"); } // Check If the Matrix is Symmentric X = XTranspose ( X = X^T) // Traverse each element in the Arrays and compare the values. for(i=0; i<rows; i++) { for(j=0; j<columns; j++) { // check if the values are not equal if(X[i][j] != XTranspose[i][j]) { // Matrices "X" and "XTranspose" are not equal printf("Matrices X & XTranspose(X^T) are Not Equal\n"); printf("Given Matrix X is not a Symmetric Matrix\n"); return 0; } } } // If we reached here, The X and XTranspose is Identical (Equal) printf("Given Matrix X is a Symmetric Matrix\n"); return 0; } |
Program Output:
Let’s compile and run the program.
Compile the program
$ gcc check-symmetric-matrix.c
Run the Program
Test 1: Normal Cases:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
$ ./a.out Enter the Row size for Matrix(1-100): 3 Enter the Column Size for Matrix(1-100): 3 Enter Elements for the Matrix(X) of Size 3X3: 2 3 6 3 4 5 6 5 9 Transpose of Maxtrix X(XTranspose = X^T) is : 2 3 6 3 4 5 6 5 9 Given Matrix X is a Symmetric Matrix $ |
From the above output, We can see that The input matrix is a Symmetric Matrix as its transpose and original matrices are equal.
Let’s look at a few more examples.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
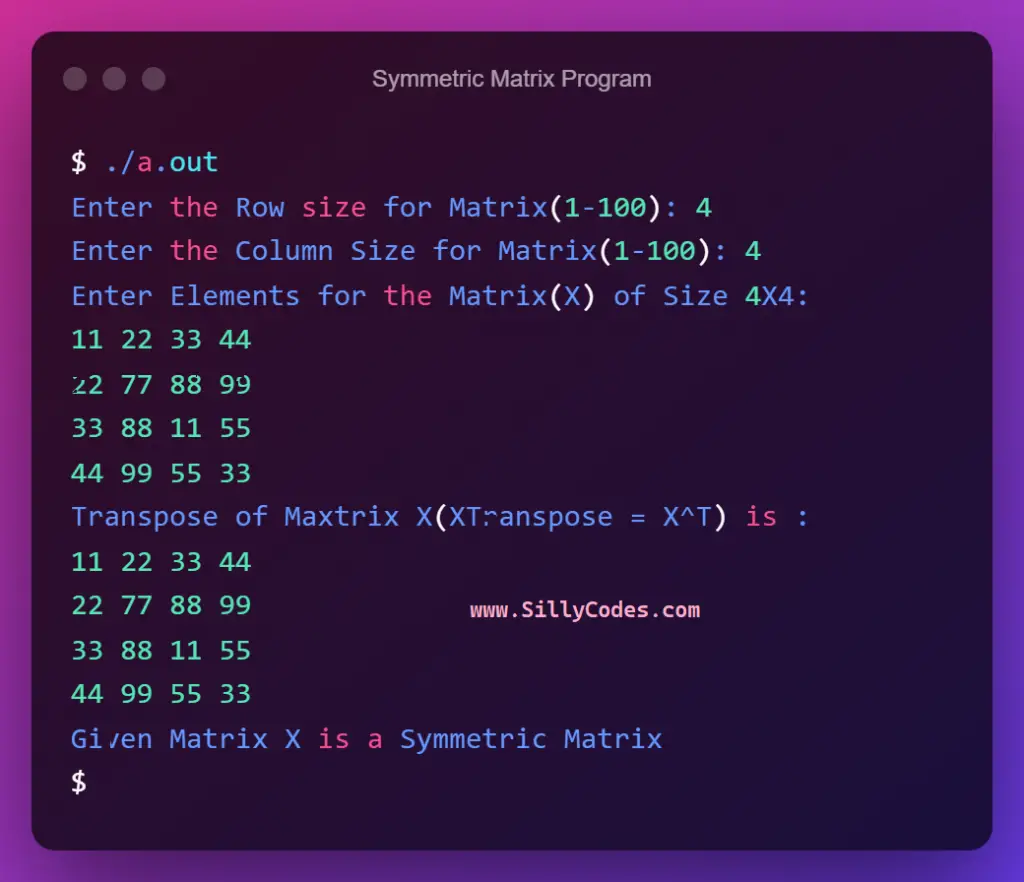
$ ./a.out Enter the Row size for Matrix(1-100): 4 Enter the Column Size for Matrix(1-100): 4 Enter Elements for the Matrix(X) of Size 4X4: 11 22 33 44 22 77 88 99 33 88 11 55 44 99 55 33 Transpose of Maxtrix X(XTranspose = X^T) is : 11 22 33 44 22 77 88 99 33 88 11 55 44 99 55 33 Given Matrix X is a Symmetric Matrix $ |
Test 2: Negative tests:
|
1 2 3 4 5 6 7 8 9 |
$ ./a.out Enter the Row size for Matrix(1-100): 5 Enter the Column Size for Matrix(1-100): 6 Symmetric Matrix is Square Matrix, Rows and Columns Must be Equal $ ./a.out Enter the Row size for Matrix(1-100): 700 Enter the Column Size for Matrix(1-100): 700 Invalid Rows or Columns size, Please Try again $ |
The program displays an error message if the input matrix is not a square matrix or if sizes go beyond the present limits.
Check Symmetric Matrix using Functions in C Program:
We have used only one function to do all the tasks in the above program. Let’s use the functions for each sub-tasks like reading the matrix from the user, printing the matrix on the console, checking the symmetric matrix, etc.
Here is the modified version of the symmetric matrix checking program using user-defined functions.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 |
/* Program to Calculate if the Matrix is Symmetric Matrix in C using Functions SillyCodes.com */ #include <stdio.h> // Define MAX ROWS and COLUMNS const int ROWS=100; const int COLUMNS=100; // Function declaration int isSymmetricMatrix(int rows, int columns, int X[rows][columns], int XTranspose[rows][columns]); /** * @brief - Read Matrix from the user and update 'A' * * @param rows - Rows in Matrix(2Darray) * @param columns - Columns in 'A' * @param A[][] - 'A' is Matrix or 2D array */ void readMatrix(int rows, int columns, int A[rows][columns]) { int i, j; for(i=0; i<rows; i++) { for(j=0; j<columns; j++) { //printf("A[%d][%d]: ", i, j); scanf("%d", &A[i][j]); } } } /** * @brief - Print the elements of the Matrix * * @param rows - Rows in Matrix(2Darray) * @param columns - Columns in 'A' * @param A[][] - 'A' is a Matrix or 2D array */ void displayMatrix(int rows, int columns, int A[rows][columns]) { int i, j; for(i=0; i<rows; i++) { for(j=0; j<columns; j++) { // Print Elements printf("%d ", A[i][j]); } printf("\n"); } } /** * @brief - Calculate Transpose of 'X' Matrix and Store it in 'XTranspose' Matrix * * @param rows - Rows in the Matrices * @param columns - Columns in the Matrices * @param X - Matrix * @param XTranspose - Transpose of 'X' Matrix * @return void */ void calculateTranspose(int rows, int columns, int X[rows][columns], int XTranspose[columns][rows]) { int i, j; // Transport the Matrix 'X' and store the result in `XTranspose' for(i=0; i<rows; i++) { for(j=0; j<columns; j++) { // Transpose X. Note, 'i' and 'j' are interchanged XTranspose[j][i] = X[i][j]; } } } int main() { // Declare two matrices. // 'X' is Input matrice // 'XTranspose' stores Transpose of 'X' int X[ROWS][COLUMNS], XTranspose[ROWS][COLUMNS]; int rows, columns, i, j; // Take the Row size and Column size from user printf("Enter the Row size for Matrix(1-%d): ", ROWS); scanf("%d", &rows); printf("Enter the Column Size for Matrix(1-%d): ", COLUMNS); scanf("%d", &columns); // Check if the matrix is square if(rows != columns) { printf("Symmetric Matrix is Square Matrix, Rows and Columns Must be Equal \n"); return 0; } else if(rows >= ROWS || rows <= 0 || columns >= COLUMNS || columns <= 0) { // check for array bounds printf("Invalid Rows or Columns size, Please Try again \n"); return 0; } // Take the user input for 1st Matrix - 'X' printf("Enter Elements for the Matrix(X) of Size %dX%d: \n", rows, columns); readMatrix(rows, columns, X); // Calculate Transpose of 'X' Matrix and Store it in 'XTranspose' Matrix calculateTranspose(rows, columns, X, XTranspose); printf("Transpose of Maxtrix X(XTranspose = X^T) is : \n"); // Note, That we are iterating over columns and then rows // As Symmentric Matrix is Square Matrix, It doesn't change anything in this case displayMatrix(columns, rows, XTranspose); // Check If the Matrix is Symmentric // Symmetric Matrix - X = XTranspose ( X = X^T) // Check if the Matrix "X" and "XTranspose" are equal int result = isSymmetricMatrix(rows, columns, X, XTranspose); // Check 'result' if(result == 1) { // The X and XTranspose is Identical (Equal) printf("Matrices X & XTranspose(X^T) are Equal\n"); printf("Given Matrix X is a Symmetric Matrix\n"); } else { // Matrices "X" and "XTranspose" are not equal printf("Matrices X & XTranspose(X^T) are Not Equal\n"); printf("Given Matrix X is not a Symmetric Matrix\n"); } return 0; } /** * @brief - Check Matrices pointed by 'X' and 'XTranspose' are equal and Symmetric Matrix * * @param rows - Rows in the Matrices * @param columns - Columns in the Matrices * @param X - First Matrix * @param XTranspose - Second Matrix * @return int - 1 if 'X' and 'XTranspose' are equal(so Symmentric Matrix), Otherwise 0 */ int isSymmetricMatrix(int rows, int columns, int X[rows][columns], int XTranspose[rows][columns]) { int i, j; // Traverse each element in the Matrices and compare the values. // Iterate over rows for(i=0; i<rows; i++) { // Iterate over the columns for(j=0; j<columns; j++) { // check if the values are not equal if(X[i][j] != XTranspose[i][j]) { // Matrices "X" and "XTranspose" are not equal // Not a Symmetric Matrix return 0; } } } // If we reached till here, Then Matrices are equal. So X is Symmetric Matrix return 1; } |
We have defined four user-defined functions in the above program (excluding the main() function)
They are
- The
readMatrix() Function.
- Prototype: void readMatrix(int rows, int columns, int A[rows][columns])
- readMatrix() function is used to read the user input and update the input matrix
- The
displayMatrix() Function
- Prototype: void displayMatrix(int rows, int columns, int A[rows][columns])
- The displayMatrix() function is used to display the elements of the matrix on the console
- The
calculateTranspose() Function.
- Prototype: void calculateTranspose(int rows, int columns, int X[rows][columns], int XTranspose[columns][rows])
- The calculateTranspose() function will calculate the transpose of the given matrix and updates the XTranspose Matrix
- The
isSymmetricMatrix() function
- Prototype: int isSymmetricMatrix(int rows, int columns, int X[rows][columns], int XTranspose[rows][columns])
- The isSymmetricMatrix() function checks if the X and XTranspose matrices are identical, Thus the X is a Symmetric Matrix.
- This function returns One(1) if the X is a Symmetric matrix, Otherwise it returns Zero(0)
Program Output:
Let’s compile and Run the Program using GCC compiler(Any Compiler)
Test 1:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
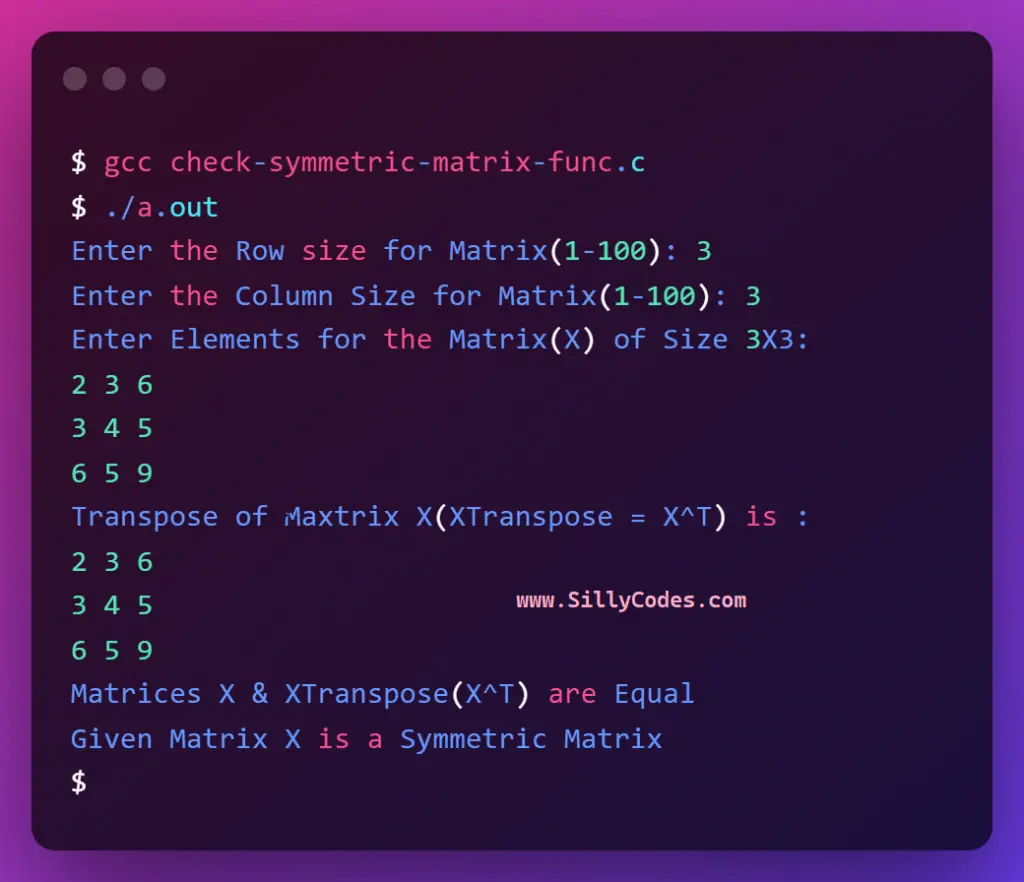
$ gcc check-symmetric-matrix-func.c $ ./a.out Enter the Row size for Matrix(1-100): 3 Enter the Column Size for Matrix(1-100): 3 Enter Elements for the Matrix(X) of Size 3X3: 2 3 6 3 4 5 6 5 9 Transpose of Maxtrix X(XTranspose = X^T) is : 2 3 6 3 4 5 6 5 9 Matrices X & XTranspose(X^T) are Equal Given Matrix X is a Symmetric Matrix $ |
Test 2:
|
1 2 3 4 5 6 7 8 9 10 |
$ $ ./a.out Enter the Row size for Matrix(1-100): 7 Enter the Column Size for Matrix(1-100): 4 Symmetric Matrix is Square Matrix, Rows and Columns Must be Equal $ ./a.out Enter the Row size for Matrix(1-100): 400 Enter the Column Size for Matrix(1-100): 400 Invalid Rows or Columns size, Please Try again $ |
As we can see from the above outputs, The program is generating the excepted results.
Related Matrices Programs:
- C Program to Read and Print Matrix or 2D Array
- C Program to demonstrate How to Pass 2D Array to Functions
- C Program to Multiplication of two Matrices
- C Program to Add Two Matrices
- C Program to Subtract Two Matrices
- C Program to Calculate the Transpose of Matrix
- C Program to Check Two Matrices are Equal
- C Program to Check Multiplicability of Two Matrices
- C Program to Check a Sparse Matrix
- Matrix and Scaler Multiplication Program in C
- C Program to Print Main Diagonal Elements of Matrix
- C Program to calculate the Sum of Diagonal Elements in a Matrix